O sistema decimal é amplamente favorecido pela simples razão de que temos dez dedos. Cada quantidade abstrata de 0 a 9 pode ser contada em cada um dos nossos dedos longos. Se os chimpanzés tivessem evoluído com doze dedos, talvez os humanos tivessem adotado o sistema duodecimal ou de base 12 para contagem. No entanto, essa inadequação não nos impediu de explorar a opção, assim como sistemas numéricos mais elevados.Os egípcios, de fato, não contavam com seus dez dedos, mas nas doze juntas entre os dedos. É uma pena que instituições inteiras sejam baseadas no sistema decimal, que ainda usamos para nossos cálculos mundanos diários, como contar dinheiro quando, como os matemáticos sugerem, o sistema de Base-12 ou o sistema dúzia se sairia muito melhor.
Maior Divisibilidade
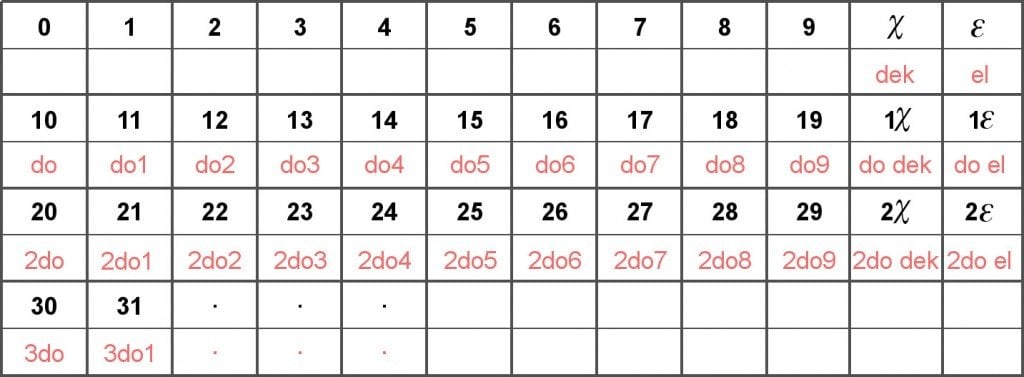
Os doze símbolos no sistema dúctil são listados como 0-1-2-3-4-5-6-7-8-9-χ (pronuncia-se ‘dek’) e ε (pronuncia-se ‘el’). O número 10 no sistema se torna 12 e é pronunciado ‘doh’. Os próximos doze números são listados com o prefixo ‘doh’ desta forma: doh-1 (11), doh-2 (12), doh-3 (13),… doh-dek (1χ), doh-el (1ε ). O número 20 é, portanto, chamado de 2-doh e os próximos números são listados com o prefixo 2-doh, de modo que 21 é pronunciado como 2-doh-1 e assim por diante até chegar a 30 ou 3-doh.
É claro que o sistema parece desconcertante no início, mas o sistema decimal ou o alfabeto também a criança que o encontra pela primeira vez. Quando nos acostumamos ao sistema, porém, começamos a perceber que seus benefícios valem a pena. Por exemplo, as crianças descobrirão que as tabelas de multiplicação de aprendizado na Base-12 são muito mais fáceis do que seriam na Base-10. Considere as tabelas de multiplicação de três, quatro e seis na Base-12.
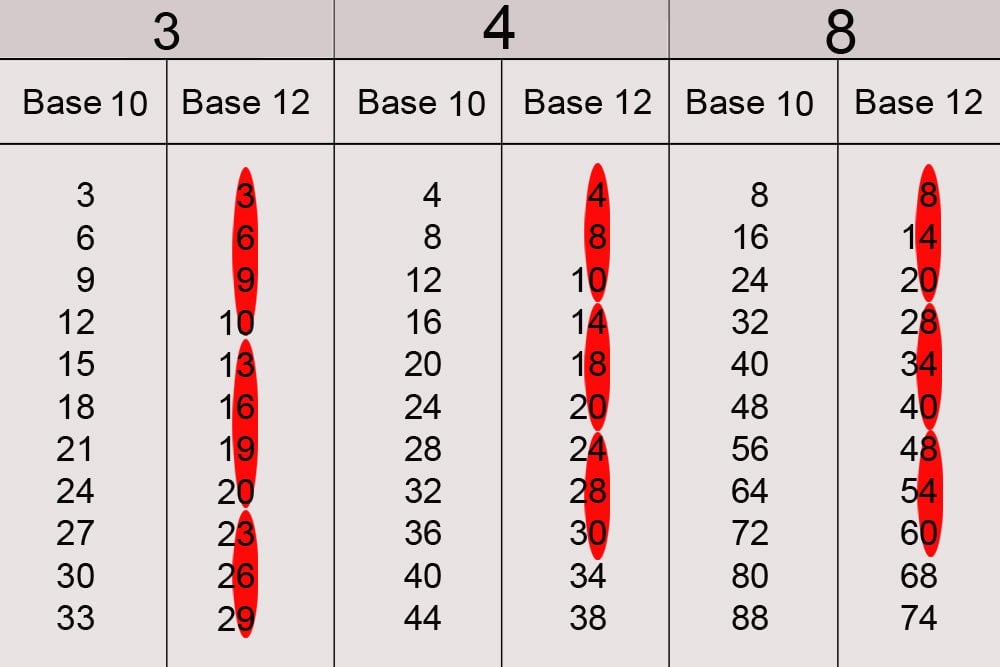
A transformação mostra que um padrão recorrente e distinto surge dentro de cada tabela, tornando-os mais fáceis de aprender.
No entanto, os matemáticos não admiram o sistema por sua aptidão para a multiplicação, mas sim por sua aptidão para a divisão. Um excelente sistema numérico é aquele que é divisível por mais números. Por exemplo, enquanto 10 é apenas divisível por 1,2, 5 e 10 em si, 12 é divisível por 1,2,3,4,6 e 12 em si. Isso facilita as oportunidades de dividir, bens ou o dinheiro que você compra com eles.
Considere dividir US $ 100 ou 100 bens em três partes iguais. Cada parte consistirá em US $ 33.3333 ou 33.3333 bens cada, uma fração universalmente desaprovada. Agora, vamos dividir o mesmo número no sistema dúbio. Agora, 1/3 é o mesmo que dividir 4/12, no entanto, 12 no sistema dúzia é 10, então, a divisão agora se torna 4/10, que é igual a 0,4, uma fração perfeitamente rígida.
Ou considere dividir $ 100 em 2/3 partes. Cada parte deve adquirir $ 0,6666 …, novamente, um número que nos perturba. Agora, vamos realizar a divisão na Base-12. A fração pode ser escrita como 8/12, que no sistema dúctil se transforma em 8/10 ou 0,8, um número não tão perturbador.

(Crédito da foto: National Park Service)
O sistema mais versátil
No entanto, pode-se argumentar que, se a divisibilidade é a virtude de um excelente sistema, não deveríamos adotar um sistema ainda maior, como o Base-200? A lógica é indiscutível; 200 é divisível por números muito maiores que 10 ou 12. Além disso, a complexidade do espaço é drasticamente reduzida, pois nos permite representar números maiores com unidades menores. No entanto, para usar o sistema de forma eficaz, é preciso lembrar de um mamute de 200 símbolos! No outro extremo, existe a Base-2 ou o sistema binário, que consiste em meros dois símbolos (1 e 0), mas requer que um número tão pequeno quanto 50 seja representado por uma longa sequência de bits: 110010. Não nos esqueçamos de que também exibe a divisibilidade mais pobre.
Um compromisso deve ser feito entre os três aspectos: tamanho do símbolo, complexidade do espaço e maior divisibilidade. Os babilônios foram os primeiros a adotar o Base-60 ou o sistema sexagesimal, que era nada menos que um gênio. O sistema consiste em menos símbolos do que os símbolos no Base-200 e exibe menos complexidade de espaço que o sistema binário. No entanto, sua característica mais lucrativa é que não só tem o mesmo número de fatores que 200 (12), mas ao contrário de 200, é tricotômica. Isso tornou o sistema mais conveniente e, portanto, mais onipresente para manter o tempo e, desde a herança dos gregos, estudar os ângulos.

(Créditos das fotos: Mike Flippo / Shutterstock)
O sistema dúzia tem a mesma vantagem. Sistemas como Base-12 ou Base-60 são, portanto, sistemas numéricos maravilhosamente versáteis. Sim, 12 tem menos fatores e maior complexidade de espaço que 60, mas ainda é tricotômico e o número de símbolos na Base-12 é bem menor do que na Base-60. Existem apenas mais dois símbolos do que os encontrados no sistema Base-10 religiosamente seguido, portanto, aprender os dois símbolos extras não é um obstáculo muito alto para ser superado. Nessa natureza, a Base-12 é realmente profunda: de todos os sistemas numéricos versáteis, é o mais fácil de aprender.
Nosso uso do sistema decimal é puramente baseado no hábito. Não é necessário sequer desaprender todo o sistema decimal; ele ou ela deve simplesmente incorporar dois símbolos adicionais na ordem existente. Mas … é tarde demais? A revolução virá com o custo enlouquecedor de reescrever a maioria dos livros de matemática já publicados. A partir de agora, isso é, sem dúvida, altamente implausível.
Falha do Decimal
Nem a adição de dois meses ao calendário original de dez meses, nem a noção de um dia e uma noite de 12 horas foram aceites em vista das virtudes dos 12, mas o efeito fortuito é evidente, no entanto. O que foi aceito em vista de suas virtudes foram as unidades de comprimentos e pesos: 12 polegadas ainda compõem um pé. No entanto, tudo foi reorganizado quando o sistema decimal foi revivido e a maioria das unidades foram métricas. De fato, por um breve período, até o tempo foi decimado.

(Crédito da foto: Flickr)
Os franceses estavam enamorados, ou melhor, obcecados pelo sistema Base-10, a ponto de inventar e seguir um cronograma de calendário não sete, mas dez dias por semana. O mês não foi dividido em quatro semanas, mas em três décadas. O pior é que eles até decompunham os dias! A duração de um dia foi legalmente reduzida de doze horas para dez, sendo que cada hora compreendeu cem minutos, cada um compreendendo cem segundos. Cada dia tinha então 100.000 segundos de duração, em comparação com os 86.400 segundos que é em um dia babilônico de 12 horas e 60 minutos-60 segundos.
Os cidadãos eram obrigados a trabalhar para não seis, mas nove dias marginalmente mais longos a cada semana! Isto era, como você poderia imaginar, assustador. Eles seguiram esse calendário peculiar e decimalizado por 12 anos após a Revolução Francesa, doze longos anos após os quais suas desvantagens não podiam mais ser ignoradas e finalmente foram descartadas de uma vez por todas.