Não, a resposta não é zero. O infinito é o maior número que existe, então o oposto do infinito seria o menor número existente. Zero significa nada, então o que estamos procurando é um número apenas maior que zero. No entanto, como descobriremos, determinar esse número não é tão simples quanto apontar para o número 1.
Infinidades são estranhas
O infinito confundiu a humanidade desde a antiguidade. É preciso perceber que o infinito não é um número concreto, mas sim uma ideia; existe apenas na abstração. O infinito não pode ser um número concreto, digamos, x, porque podemos, pela lógica da adição, adicionar 1 a x e criar um novo infinito. Podemos então adicionar outro 1 para criar um infinito maior. Podemos, de fato, adicionar infinito ao infinito para criar talvez o infinito de todos os infinitos, mas então podemos adicionar a este infinito outro 1 e … você sabe o que fazer.

Infinidade. (Crédito: Anthony Jauneaud / Flickr)
O reino microscópico não é diferente. O oposto do infinito é chamado infinitesimal e sua natureza é igualmente bizarra. Ao contrário dos números inteiros, os números reais não são rígidos. Sua natureza fragmentada nos permite encontrar e criar números infinitos entre quaisquer dois números. Um número pode ser combinado quantas vezes puder ser dividido. Poderia haver uma centena de números entre 0 e 1, de 0,01-0,99, ou até milhões, um só tem que adicionar zeros após o ponto decimal – dividir cada vez mais para criar novos números. Assim, enquanto 0,00000000000000001 parece infinitesimal, pode-se apenas dividi-lo por 10 para criar um novo infinitesimal – 0,000000000000000001.
Assim, infinitesimal, como o infinito, existe apenas na abstração, mas sua natureza incerta é muito desconcertante não apenas para os matemáticos, mas também para os físicos.
Erros Infinitesimais
A matemática é a linguagem que usamos para expressar nossas idéias em física, então uma inconsistência na matemática se traduz em uma inconsistência na física, em nosso conhecimento da natureza – da realidade. A inconsistência surge da nossa incerteza do valor infinitesimal, que tem sido usado para derivar muitas fórmulas cruciais. De fato, todo um ramo da matemática é baseado em infinitesimal, sem o qual, o progresso na física teria sido lento.
Uma fórmula que consigo pensar é a área de um círculo. Kepler calculou a área de um círculo dividindo-o em triângulos. A área do círculo, portanto, seria a soma das áreas de cada triângulo. Um círculo pode ser dividido em quatro triângulos com dois diâmetros, no entanto, os lados desses triângulos não se aproximam das curvas adequadamente, excluindo algum espaço, então a área calculada é errônea.
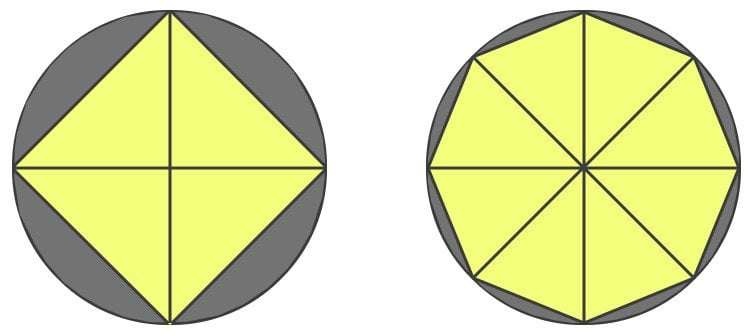
Para reduzir esse erro, podemos desenhar mais diâmetros para criar mais triângulos de lados menores. No entanto, o erro é reduzido dessa maneira, mas ainda é finito. Então, nós ainda dividimos o círculo em mais e mais triângulos até que não haja espaço deixado excluído. No entanto, para eliminar completamente esse erro, devemos dividi-lo em um número infinito de triângulos. Agora, porque uma linha pode ser interpretada como parte de um círculo imenso, podemos dizer que nosso círculo é composto de linhas infinitas, que são aproximadas pelas bases infinitesimais de nossos infinitos triângulos.
Pode-se notar que a seqüência de triângulos é remanescente de um fã chinês. Todos os triângulos ocupam uma área igual, mas podemos converter o ventilador em um grande triângulo retângulo distribuindo ou esticando essa área. Seus perímetros mudaram, mas a área total permanece a mesma. A altura deste triângulo, com o cume sendo o centro do círculo, é o comprimento do leque – o raio do nosso círculo e a base, a circunferência do círculo. A área é ½ vezes a altura vezes a base, que é ½ vezes r vezes 2πr, ou πr².
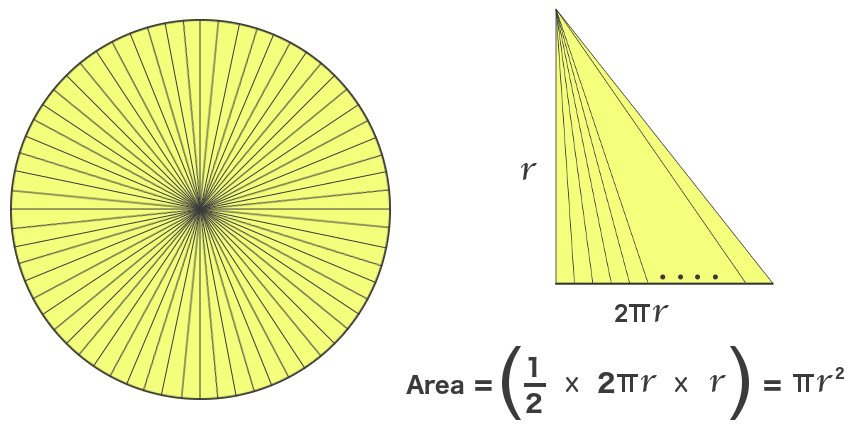
Triângulos infinitos triângulo de ângulo reto e cálculo
Esta é, obviamente, a resposta correta, mas o resultado ainda é errôneo. As bases devem ser verdadeiramente infinitesimais, por isso mesmo que o Kepler desenhe triângulos realmente muito finos, sabemos que ele poderia ter desenhado mais. No momento em que ele para de desenhar triângulos, ele deixa para trás espaços, mesmo que realmente pequenos, mas ainda finitos. As curvas são então aproximadas de forma inadequada e o cálculo da área do círculo é um pouco errôneo. Embora isso possa deixar um matemático desconfortável, a maioria “ignora” essas diferenças, pois, como vimos, os resultados obtidos não são incorretos.
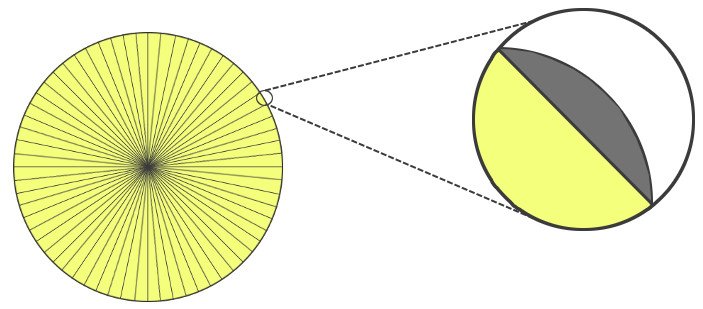
O cálculo, inventado ou descoberto por Leibniz e Newton independentemente, também foi fundado em infinitesimais. Esse ramo da matemática está preocupado com a mudança, com curvas. Por exemplo, quando integramos uma função, basicamente calculamos a área sob a curva que ela desenha. No entanto, como calcular a área de um círculo, calculamos aproximando a curva com retângulos infinitamente finos. Quanto mais finos os retângulos, menor o erro.
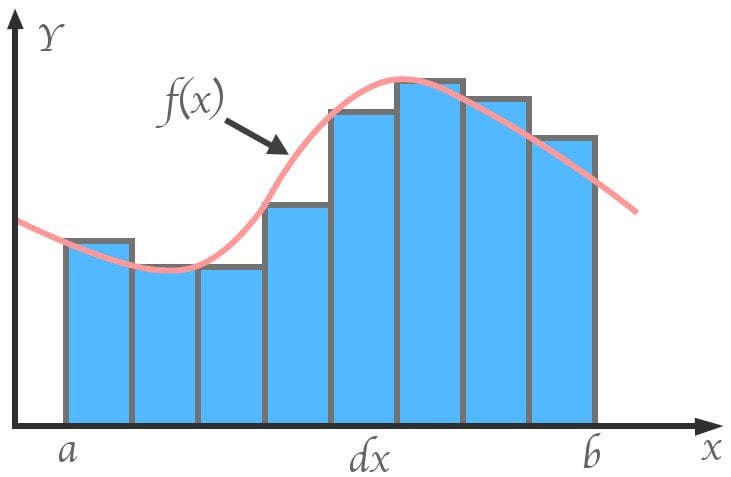
A área de um retângulo é o produto de seu comprimento – o valor no eixo Y naquele ponto da curva e sua largura – a unidade infinitesimal que chamamos de ‘dx’. Calculamos a área de cada retângulo e somamos para determinar a área sob a curva. Isso é muito útil em física; por exemplo, a área sob a curva de velocidade de um corpo dá o valor de seu deslocamento, mas o resultado não deveria ser errôneo, assim como a área do círculo era?
Esse problema inerradicável e insolúvel incomodou os matemáticos por dois séculos após o advento do cálculo, até que o conceito de limites fosse refinado. Os limites estavam implícitos no trabalho de Newton e Leibniz, mas foram modificados e redefinidos mais tarde no início do século XIX. As novas ideias eram matematicamente rigorosas e consistentes. Os detalhes estão além do escopo deste artigo, mas os limites permitiram que os matemáticos finalmente se livrassem dos infinitesimais para sempre. O que ainda não nos livramos é o absurdo que é o infinito.