Por que uma bala de canhão disparada de um canhão não desce verticalmente, mas sim curvilínea? Por que um dardo lançado lança um arco sumptuoso antes de picar o chão? Independentemente da natureza do projétil, o arco que se desenha através do ar é precisamente uma parábola.A razão é, obviamente, a gravidade , a única força que afeta seu movimento (negligenciando a resistência do ar) depois de projetada. No entanto, o que estamos essencialmente perguntando é, por que a força da gravidade traça uma parábola? Kepler sabia que os planetas orbitavam o Sol em uma elipse, mas ele não sabia por que eles o faziam. Na mesma linha, por que um projétil não traça qualquer outra forma além de uma parábola?
A equação
Claro, isso não é verdade quando um projétil é projetado perpendicularmente à superfície da Terra. Para observar uma trajetória parabólica, devemos projetá-la em algum ângulo com a superfície. Mesmo que nenhuma força horizontal afete um projétil após seu lançamento, é a força horizontal inicial que possibilita a jornada gloriosa. De que outra forma um javelim poderia percorrer uma distância horizontal se não fosse dotado de uma força horizontal?
No século XVII , a humanidade ainda tinha que construir um foguete e os telescópios mais poderosos não poderiam olhar além de Saturno. Apesar dessas restrições, como Newton, isolado em uma minúscula sala na Inglaterra, descobriu que os planetas orbitam o Sol e não – como os filósofos mais eminentes da época acreditavam (ou esperavam) – em um círculo, mas sim uma elipse? Matemática, claro.
Newton provou a afirmação de Kepler descobrindo uma relação entre a distância entre a Terra e o Sol, e o ângulo que ela atravessa enquanto gira em torno dela. Ele descobriu que era exatamente o mesmo relacionamento que descreve um ponto traçando uma elipse. No entanto, sua avaliação foi baseada em sua recém proposta lei da gravidade. Se sua lei não fosse verdadeira, sua prova também se desmoronaria. Agora sabemos que o que ele propôs era verdadeiro; Newton nunca explicou o que é a gravidade , mas explicou muito bem como isso funciona.
Da mesma forma, para determinar a curva que um projétil traça, devemos encontrar uma equação que descreva seu movimento e a curva que corresponde a ele.
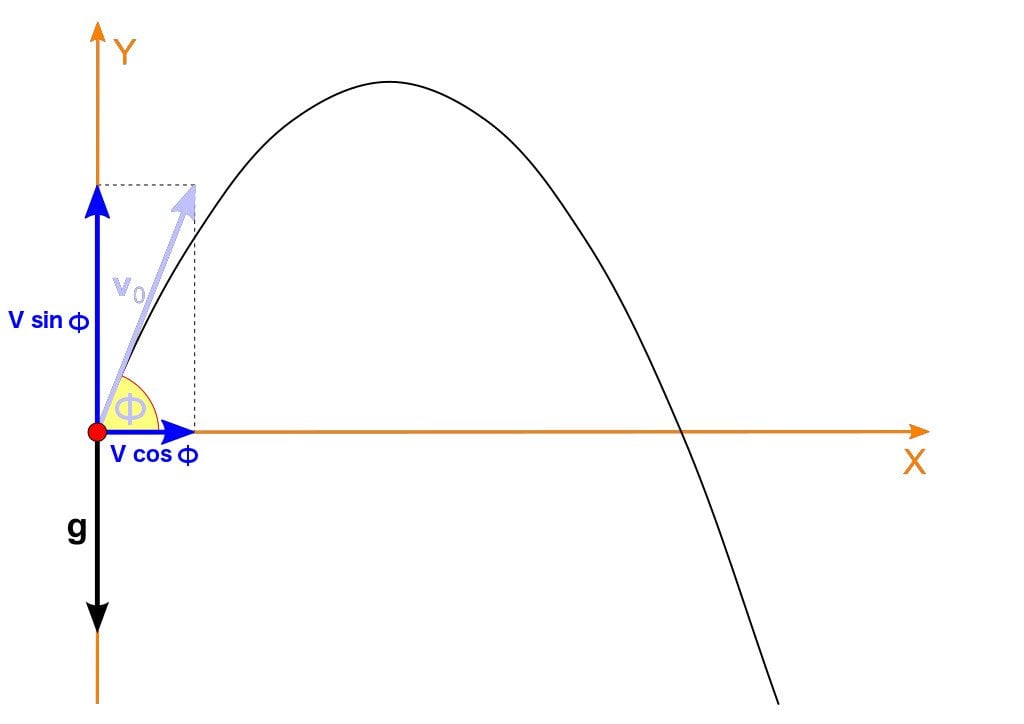
(Crédito da foto: Sándor Zátonyi / Wikimedia Commons)
O projétil é projetado com uma velocidade inicial ‘v’ em um ângulo ‘Φ’ em relação à superfície. A distância que o projétil percorre horizontalmente (no eixo X) é dada como x = vtcosΦ (v = x / t). No entanto, a distância percorrida verticalmente (no eixo Y) é dada como y = vtsinΦ – (½) gt² . Isso ocorre porque, na vertical, o projétil experimenta uma força e, portanto, aceleração, a saber, a aceleração devida à gravidade, denotada por ‘g’.
Agora, como essa aceleração é constante, podemos usar a equação cinemática s = ut + (½) at ² para calcular a distância ‘y’. Aqui, ‘u’ é a velocidade inicial, que neste caso é vsinΦ e ‘a’ é a aceleração constante, que neste caso é ‘-g’, devido à nossa convenção selecionada. Portanto, a distância vertical y = vtsinΦ – (½) gt² .
Para encontrar ‘y’ em termos de ‘x’, ou para obter uma equação que descreva a relação entre ‘y’ e ‘x’, resolvemos para ‘t’ na primeira equação e substituímos seu valor em ‘y’.
ou,
Substitua o valor de t em:
Aqui, tanΦ e g / 2v²cos²Φ são constantes, então a equação estranhamente se assemelha à equação y = ax + bx² – a equação de uma parábola!